Círculo unitario y funciones trigonométricas de un ángulo en general.
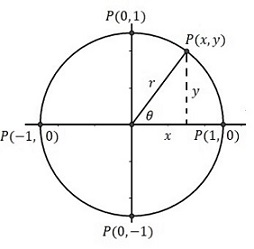
Para un ángulo \(\theta\) en posición normal como se muestra en la figura de la izquierda y el punto \(P(x,y)\), del hecho que el punto \(P(x,y)\) puede estar en cualquier parte sobre la circunferencia, entonces las seis funciones trigonométricas del ángulo \(\theta\) se definen como sigue: \begin{array}1 1)~\sin{\theta}=\frac{y}{r} &2)~\cos{\theta}=\frac{x}{r} &3)~\tan{\theta}=\frac{y}{x}\\ 4)~\cot{\theta}=\frac{x}{y}&5)~\sec{\theta}=\frac{r}{x}&6)~\csc{\theta}=\frac{r}{y}\end{array} De las expresiones para seno y coseno del ángulo se tiene que, $$x=r\cos{\theta}\ \ \ \ \ \ y=r\sin{\theta}$$ en consecuencia, si \(r=1\) entonces \(y=\sin{\theta}; \ \ \ \ x=\cos{\theta}\) las cuales son llamadas coordenadas polares de \(x\) y \(y\).
Funciones de ángulos en el plano cartesiano.
Con base en análisis del círculo unitario centrado en el origen de coordenadas \(x^2+y^2=1\) se pueden establecer las funciones trigonométricas de un ángulo cualquier en el plano, cuyo lado terminar pasa por un punto \(P(x,y).\) Comience por observar los signos de cada una de las funciones tomando en cuenta que para cualquier valor de \(r\), se tiene, \(x=r\cos{\theta},\ \ y=r\sin{\theta}\) de aquí se deduce el análisis siguiente:
Cuadrante |
\(\textcolor{navy}{\mathrm{\underline{Signo~ de~ las~ funciones~trigonométricas.}}}\) |
||
|---|---|---|---|
Positiva |
Negativa |
||
Primer |
Todas positivas |
||
Segundo |
\(\sin{\theta},\ \csc{\theta}\) |
\(\cos{\theta},\tan{\theta},\ \cot{\theta},\sec{\theta}\) |
|
Tercero |
\(\tan{\theta},\ \cot{\theta}\) |
\(\sin{\theta},\cos{\theta},\ \sec{\theta},\csc{\theta},\) |
|
Cuarto |
\(\cos{\theta},\ \sec{\theta}\) |
\(\sin{\theta},\tan{\theta},\ \cot{\theta},\csc{\theta}\) |
|
Usando los resultados obtenidos hasta ahora y el círculo unitario se obtienen los valores para las funciones de \(0°,~90°,~180°,~270°\) y \(360°\) de donde se construye la siguiente tabla resumen.
\(\textcolor{navy}{\theta}\) |
\(\textcolor{navy}{30°}\) |
\(\textcolor{navy}{60°}\) |
\(\textcolor{navy}{45°}\) |
\(\textcolor{navy}{0°}~{\rm y}~\textcolor{navy}{360°} \) |
\(\textcolor{navy}{90°}\) |
\(\textcolor{navy}{180°}\) |
\(\textcolor{navy}{270°}\) |
\(\textcolor{navy}{\sin{\theta}}\) |
\(\frac{1}{2}\) |
\(\frac{\sqrt3}{2}\) |
\(\frac{\sqrt2}{2}\) |
\(0\) |
\(1\) |
\(0\) |
\(-1\) |
\(\textcolor{navy}{\cos{\theta}}\) |
\(\frac{\sqrt3}{2}\) |
\(\frac12\) |
\(\frac{\sqrt2}2\) |
\(1\) |
\(0\) |
\(-1\) |
\(0\) |
\(\textcolor{navy}{\tan{\theta}}\) |
\(\frac{\sqrt3}3\) |
\(\sqrt3\) |
\(1\) |
\(0\) |
no existe |
\(0\) |
no existe |
\(\textcolor{navy}{\cot{\theta}}\) |
\(\sqrt3\) |
\(\frac{\sqrt3}3\) |
\(1\) |
no existe |
\(0\) |
no existe |
\(0\) |
\(\textcolor{navy}{\sec{\theta}}\) |
\(\frac{2\sqrt3}3\) |
\(2\) |
\(\sqrt2\) |
\(1\) |
no existe |
\(-1\) |
no existe |
\(\textcolor{navy}{\csc{\theta}}\) |
\(2\) |
\(\frac{2\sqrt3}3\) |
\(\sqrt2\) |
no existe |
\(1\) |
no existe |
\(-1\) |
Ejemplo. Determinar todas las funciones trigonométricas del ángulo theta, dadas las condiciones siguientes.
$$1.~~\cot{\theta=\frac{3}{2}}~~ \mathrm{donde}~~180°\leq \theta \leq 270°$$
$$2.~~\csc{\theta}=-\frac{5}{7}~~ \mathrm{donde}~~270°\leq \theta \leq 360°$$
$$3.~~\sec{\theta}=-{\frac{5}{4}} ~~\mathrm{donde}~~90°\leq \theta \leq 180°$$
Solución 1: para escribir las funciones se necesita conocer los valores de \(x,\ y\ ,r,\) de donde,
$$x=r\cos{\theta};\ \ \ y=r\sin{\theta};\ \ r=\sqrt{x^2+y^2}$$
y además considerar sus signos.
$$\cot{\theta}=\frac{3}{2}=\frac{x}{y}~~ \mathrm{de~ donde~} r=\sqrt{3^2+2^2}=\sqrt{13}$$
Para \(\theta\) en el tercer cuadrante:
\begin{align}
\sin{\theta}&=-\frac{y}{r}=-\frac{2}{\sqrt{13}}=-2\frac{\sqrt{13}}{13}&\csc{\theta}&=-\frac{r}{y}=-\frac{\sqrt{13}}{2}\\
\cos{\theta}&=-\frac{x}{r}=-\frac{3}{\sqrt{13}}-\frac{3\sqrt{13}}{13}&\sec{\theta}&=-\frac{r}{x}=-\frac{\sqrt{13}}{3}\\
\tan{\theta}&=\frac{y}{x}=\frac{2}{3}&\cot{\theta}&=\frac{x}{y}=\frac{3}{2}\\
\end{align}
Solución 2: \(\csc{\theta}=-5/7=r/y\), pero \(r\) debe ser mayor que \(y\) ya que en ningún triángulo rectángulo la hipotenusa es menor que un cateto, por tanto ningún ángulo \(\theta\) cumple la condición \(\csc{\theta}=-5/7\) y este inciso no tiene solución.
Solución 3: \(\sec{\theta}=-5/4=r/x\Longrightarrow y=\sqrt{5^2-4^2}=3,\) para \(\theta\) en el segundo cuadrante se tiene: \begin{align} \sin{\theta}&=\frac{y}{r}=\frac{3}{5}&\csc{\theta}&=\frac{r}{y}=\frac{5}{3}\\ \cos{\theta}&=-\frac{x}{r}=-\frac{4}{5}&\sec{\theta}&=-\frac{r}{x}=-\frac{5}{4}\\ \tan{\theta}&=-\frac{y}{x}=-\frac{3}{4}& \cot{\theta}&=-\frac{x}{y}=-\frac{4}{3}\\ \end{align}
